Modeling¶
Introduction¶
Modeling is an important task in mathematics, computer science and science in general. It is the process of breaking down a complex problem or situation and converting it into something that can be manipulated with equations. In terms most fifth graders would know, it is solving word problems!
Word problems may bring back nightmares for some of you but really this is how math is applied. An honest student will bemoan word problems and then ask when are we ever going to use this math during the same lecture. In actuality this student is just not looking forward enough into how the topic is currently being applied. Through the course of this text we need to see forward and accept that anything we learn will be applied. From calculus to deep learning, we will be applying our techniques.
One of the thoughest things to learn is grit. The ability to stick with a problem can be very challenging. People with grit fair much better in the world and especially in the sciences. Genius may get you a solution to some problems but grit can get you over the hump on many more.
Theory¶
Following Dr. Polya, we consider 4 steps to solving any mathematical problem
Understand the problem and clearly see what is required
Plan how the unknown is linked to the data
Carry Out our plan
Look Back at our solution and ask did it solve our original problem
We will attempt to apply these techniques of modeling to everything done throughout this course.
Let’s apply these ideas to some familiar examples from different branches of mathematics.
Examples¶
Calculus and The Cow¶
A farmer wants to enclose a pasture with 1000 yards of barbwire he found in the barn. There is a straight creek along one side of the pasture that will not need to be fenced in a rectangular fashion. If they must enclose the other three sides, what dimensions will create the largest possible area for the cows to graze?
Many of you will have seen a problem of this type before in a calculus class. But let’s work it out following our process.
First we need to understand. So we know that there is a creek running along one side of the pasture and we are going to fence in the other three sides. One of the things that always helps me understand is a picture!
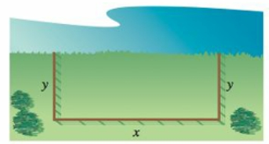
We see that if we are going to have a rectangle, two of the sides will be equal, let’s call them \(y\) and the third will be a new size, let’s call \(x\).
Next, move into the plan. What makes up the 1000 yards and what are we trying to maximize? The perimeter (minus the river side) is the 1000 yards and the area of the rectangle is what we are tring to maximize.
Still thinking about the plan, we should ask what it takes to maximize? Well in calculus we learn that if we have a function \(f(x)\) and we take the derivative and set it equal to zero, \(f'(x)=0\). The \(x\)’s that solve that equation will be critical points, candidates for the maximum. Furthermore we know that if \(x^*\) is a critical point and \(f''(x^*)<0\) Then the (local) maximum, \(f(x^*)\) occurs at \(x^*\).
Moving into the carry out phase. We have two equations but neither has been written as \(f(x)\) so how are we supposed to preform calculus on it!? Keeping in mind that we want to maximize the area, that should be our candidate for \(f(x)\). If I just try to write \(A = f(x)\), I’ll have a problem though, \(A\) depends on \(x\) and \(y\). If I write that out \(A(x,y)\). Now some of you may know how to deal with this multivariate calculus but those techniques are not required if we use the first equation, \(2y +x = 1000\) or \(y = \frac{1000-x}2\). Then $\( A(x,y) = A(x) = x\cdot\frac{1000-x}2 = 500x-\frac12x^2. \)$
import matplotlib.pyplot as plt
import numpy as np
def A(x):
return 500*x - x**2/2
x = np.arange( 0,1000,1)
plt.plot(x,A(x))
plt.title("Graph of " r'$A(x)$')
plt.show()
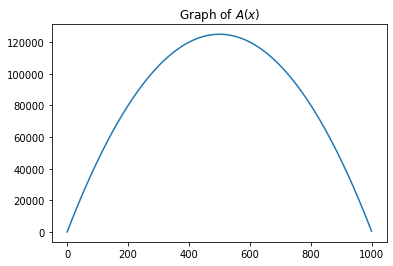
So the function we want to maximize is \(A(x) = 500x-\frac12x^2\). Recalling our power rule of calculus $\( A'(x) = 500 - x \)\( So the critical \)x^*\( is \)500\(. The second derivative is \)\(A''(x) = -1\)\( So this gives a (local) maximum of \)A(500) = \frac12 \cdot500^2$.
1/2*500**2
125000.0
Lastly, let’s look back.
Is it feasible that \(x = 500\)? Yes, that would leave \(500\) yards of barbwire for the other two sides.
Can we make a bigger area? What if \(x =400\), then \(y=300\) and \(A = 120000\). No, that isn’t any bigger!
If I found \(y = 500\) would that have been reasonable? No, that would have left nothing for the \(x\) run of the pasture.
This step is oft forgotten in claculus class but it will be very important to check that your answer is reasonable here!
How Tall is My Tree¶
There is a large tree in my yard that I would like to know the height of. Unfortunately I am not a very good climber! I do have a very large tape measurer, a partner and a good eye.

First I should try a rough estimate. I could simply see how many stick figures it takes to get to the top of the tree.

Roughly I could guess that the tree is four times the height of a person. Often this would be enough.
If I wanted to get more acurate, I could apply some trigonometery and use my tape measurer. First method I try is a similar triangles approach.
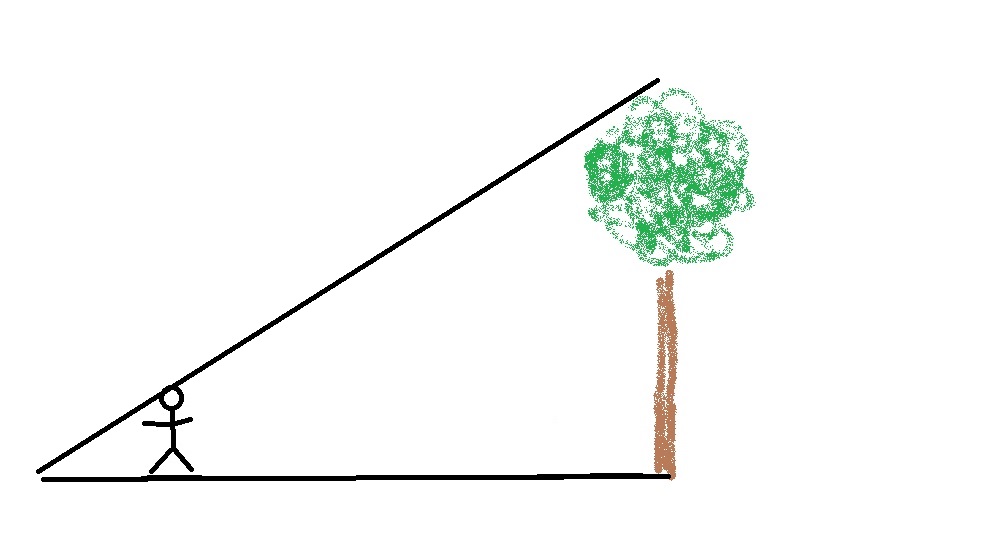
How Many Squares on the Checker Board¶
How many squares are there on a checker board? Well I don’t know about you but I’d probably just get one out and start counting. If you try this you might say something like 64 (assuming you counted correctly). But is that all the squares? What about the board itself? What about a two by two square?

So if we understand the problem we can try to make our plan. Let’s plan to examine squares of different sizes, 1X1, 2X2 all the way to 8X8. The two by two squares can overhang previous ones so we should be careful how we count them. I start to look at that and think I might make a mistake… Maybe I should go the other way to carry out! Let’s get a table of all the different sizes we are going to have to count.
Size |
1X1 |
2X2 |
3X3 |
4X4 |
5X5 |
6X6 |
7X7 |
8X8 |
|---|---|---|---|---|---|---|---|---|
Number |
64 |
1 |
I filled in the two obvious ones. But how many 7X7 can I get in there? No matter where I put it, it’ll have to be in one of the corners but not touch any of the others so that would make 4. Okay not too bad, maybe we can try the 6X6. It’ll be bigger but if we are clever, we’ll see that three off them fit across the top, three in the middle and three at the bottom. Let’s update our table
Size |
1X1 |
2X2 |
3X3 |
4X4 |
5X5 |
6X6 |
7X7 |
8X8 |
|---|---|---|---|---|---|---|---|---|
Number |
64 |
9 |
4 |
1 |
Do you see a pattern emerging? I see a bunch of perfect squares! My guess is that the 2X2 should have 49 squares in it. If I try to logic it out, I see that I can fit 7 in across the top (try it!) Then down I could get 7 rows of 7 squares and I arrive at 49. Awesome! Let’s finish the table!
Size |
1X1 |
2X2 |
3X3 |
4X4 |
5X5 |
6X6 |
7X7 |
8X8 |
|---|---|---|---|---|---|---|---|---|
Number |
64 |
49 |
36 |
25 |
16 |
9 |
4 |
1 |
All that is left is to sum them, let’s have python do it for us!
sum = 0
for i in range(1,9):
sum += i**2
sum
204
204 squares on a checkerboard! Lastly looking back, we think this answer covers all the possible squares on the checkerboard!
References¶
How to Solve It G. Polya Second Edition Princeton University Press 1957
Thinking Mathematically J. Mason Addison-Wesley Publishing Company 1985
Grit: The Power of Passion and Perseverance A. Duckworth Scribner Book Company 2016
Problems¶
How many rectangles are there in 8X8 checker board?
Re-examine the cow’s pen if the river was removed.
Re-examine the cow’s pen if two sides already had fencing.
Repeat the measurment of the tree if the person taking the measurements was standing on a slope of 3%.
Project Ideas¶
Optimal Boxes¶
Most likely there are several boxes laying around your home. Gather the measurements of one of them constructed in a three deimensional shape. Does it maximize the volume? Flatten the box and consider the two dimensional shape. Does the shape maximize the volume butt minimize the material required to fold it into a proper box?
Moore’s Law¶
Assume that the speed of new computers costing a certain amount of money grows exponentially over time, with the speed doubling every 18 months. Suppose you need to run a very time consuming program and are allowed to buy a new computer costing a fixed amount on which to run the program. If you start now, the program will take 12 years to finish. How long should you delay buying the computer and starting the program so that it will finish in the shortest amount of time from now? Also, what will the shortest finishing time be?
DIFUSE First Order System Project¶
Use python to analize the data. Differential Equations Models
